Как в Excel решить систему линейных уравнений. Решаем уравнения путем подбора параметра в Excel Как решать примеры в экселе

Текст работы размещён без изображений и формул.
Полная версия работы доступна во вкладке "Файлы работы" в формате PDF

ВВЕДЕНИЕ

Постановка проблемы и актуальность исследования . Школьный курс математики, начиная с начальной ступени и до 11 класса, включает в себя большое количество способов решения различных видов уравнений и систем уравнений. Некоторые уравнения решаются нестандартными методами, которые применить может небольшая часть выпускников школ. Анализ изученной литературы показал, что уравнения и системы уравнений встречаются в различных отраслях промышленности и экономики. И как правило, эти уравнения выглядят не так привлекательно, как школьные, и имеют нецелые решения. Чтобы автоматизировать процесс решения уравнений и систем уравнений, мы решили найти способы с помощью электронных таблиц. Электронные таблицы широко используются в профессиональной деятельности специалистов самых разных областей науки, производства и сферы услуг, в различных государственных и коммерческих организациях и фирмах. Кроме того, электронные таблицы могут быть использованы при решении бытовых задач, таких, как создание домашней картотеки книг или компакт-дисков, ведение учета коммунальных платежей или домашнего бюджета и т.п.

К настоящему времени существует достаточное количество различных учебных материалов, где подробно раскрываются способы решения производственных задач с помощью уравнений и систем уравнений , а также методы их решения с помощью электронных таблиц .

Тем не менее, в ходе исследования было обнаружено, что недостаточно исследованы способы решения уравнений высших степеней, а также уравнений, имеющих бесконечное множество решений (например, тригонометрических).

Актуальность обозначенной проблемы определила выбор темы исследования: «Решение уравнений средствами приложения Microsoft Excel».

Цель работы : исследовать инструменты приложения Microsoft Excel для решения уравнений разного порядка.

Объект исследования : приложение Microsoft Excel.

Предмет исследования : применение инструментов ПОДБОР ПАРАМЕТРА и ПОИСК РЕШЕНИЯ приложения Microsoft Excel при решении уравнений.

Гипотеза исследования: использование инструментов приложения MS Excel ПОДБОР ПАРАМЕТРА и ПОИСК РЕШЕНИЯ значительно упрощает процесс решения уравнений различного вида.

Задачи исследования :

Изучить литературу по применению уравнений при решении производственных задач.

Изучить литературу по использованию приложения Microsoft Excel в практической деятельности.

Рассмотреть способы решения уравнений с помощью инструментов ПОДБОР ПАРАМЕТРА и ПОИСК РЕШЕНИЯ приложения Microsoft Excel.

Создать видеокурсы по решению различных видов уравнений.

Теоретическая значимость : проведен анализ ряда источников по возможностям приложения Microsoft Excel при решении уравнений разного порядка.

Практическая значимость : предложены способы решения уравнений высших порядков и тригонометрических уравнений с помощью приложения MS Excel, систематизирован и обобщен материал в форме видеокурсов.

Методы исследования : теоретический анализ и обобщение научной литературы и материалов сети Интернет; проведение экспериментов по решению уравнений различного вида с помощью инструментов Подбор параметра и Поиск решения; создание видеокурсов по использованию инструментов Подбор параметра и Поиск решения при решении различных уравнений.

УРАВНЕНИЯ В РАЗЛИЧНЫХ ОТРАСЛЯХ

В современном обществе уравнения нашли свое применение во многих отраслях хозяйства и производства, а также практически во всех новейших технологиях. Конечно, математика, как и любая другая наука, не стоит на месте. Уже выработано достаточно способов решения различных видов уравнений различных степеней. Появление компьютеров и стремительное развитие информационных технологий позволило в несколько раз упростить задачи нахождения корней различных уравнений. В данной главе, в качестве примеров, нами представлены виды уравнений, решаемых в некоторых отраслях хозяйства и производства.

1.1. Уравнения при решении экономических задач

Пример 1.1.1. Рассчитать, с какого возраста необходимо уплачивать по 1000 рублей в качестве дополнительных страховых взносов, чтобы получить прибавку к пенсии в 2000 рублей за счет участия в государственной программе софинансирования?

Входные данные:

ежемесячные отчисления - 1000 руб.;

период уплаты дополнительных страховых взносов - расчетная величина (пенсионный возраст (в примере - для мужчины) минус возраст участника программы на момент вступления);

пенсионные накопления - расчетная величина (накопленная за период участником сумма, увеличенная государством в 2 раза;

ожидаемый период выплаты трудовой пенсии - 228 мес. (19 лет);

желаемая прибавка к пенсии - 2000 руб.

пенсионные накопления - расчетная величина (накопленная за период участником сумма, увеличенная государством в 2 раза).

Пусть х - возраст, с которого необходимо производить отчисления. Тогда прибавка к пенсии (в размере 2000 рублей) будет рассчитана по формуле:

Получили линейное уравнение, в котором необходимо найти параметр x .

Пример 1.1.2. Пусть дана структура цены договора: собственные расходы, прибыль, НДС. Известно, что собственные расходы составляют 150 000,00 руб., НДС 18%, а целевая стоимость договора 200 000,00 руб. Необходимо подобрать такое значение прибыли, при которой стоимость договора равна Целевой (то есть Расхождение должно равняться нулю) .

Пусть х - прибыль. Тогда цену продукции будем рассчитывать как сумму Собственных расходов и Прибыли: 150000+х. НДС от цены продукции будет равен (150000+х)*0,18. Стоимость договора вычислим как сумму Цены продукции и НДС: (150000+х)+ (150000+х)*0,18=(150000+х)*1,18.

Итак, получили уравнение (150000+х)*1,18=2000.

Пример 1.1.3. , решение которого также сводится к линейному уравнению. Определить максимальную сумму кредита, которую мы можем себе позволить взять в банке, если известно, что ежемесячно мы можем выплачивать сумму в размере 1 800,00 руб. Известны также процентная ставка по кредиту и срок, на который мы хотим взять кредит (количество месяцев) .

Пример 1.1.4 , решение которого сводится к системе линейных уравнений. Предприятию для изготовления наборов елочных украшений необходимо изготовить их составные части - шар, колокольчик, мишура .

В свою очередь для изготовления этих составных частей необходимы три вида сырья - стекло (в г), папье-маше (в г), фольга (в г), потребности в котором отражены в таблице.

Требуется:

1) определить потребности в сырье для выполнения плана по изготовлению комплектов первого, второго, третьего и четвертого вида в количестве соответственно x 1 , x 2, x 3 и x 4 штук;

2) провести подсчеты для значений x 1 = 500, x 2 = 400, x 3 = 300 и x 4 =200.

Для решения данной задачи необходимо найти корни системы линейных уравнений:

y 1 = 5· (5x 1 + 6x 2 + 8x 3 + 10x 4) = 25x 1 + 30x 2 + 40x 3 + 50x 4

y 2 = 4· (3x 1 + 4x 2 + 6x 3) = 12x 1 + 16x 2 + 24x 3

y 3 = 3· (5x 1 + 6x 2 + 8x 3 + 10x 4) + 75· (3x 2 + 5x 3 + 8x 4) = 15x 1 + 243x 2 + 399x 3 + 630x 4

Уравнения в электроэнергетике

Рассмотрим применение уравнений в электроэнергетике .

Пример 1.2.1. Приведена схема электрической цепи постоянного тока. Найти токи в ветвях цепи.

Для решения данной задачи необходимо составить и решить систему линейных уравнений на основе законов Кирхгофа (здесь не рассматривается процесс составления системы уравнений):

Уравнения в транспортной отрасли

Пример 1.3.1. Для решения задач проектирования транспортных сооружений и принятия обоснованных решений при планировании, контроле и управлении технологическими процессами дорожного строительства необходимо выявлять взаимосвязи между параметрами, определяющими ход этих процессов, и представлять их в количественной форме - в виде математических моделей. В связи с этим на практике часто применяется регрессионный анализ.

Регрессионный анализ - метод моделирования измеряемых данных и исследования их свойств путем выявления взаимосвязи между зависимой переменной y и одной или несколькими независимыми переменными x 1, x 2, ..., xn.

Независимые переменные иначе называют факторами, аргументами, или регрессорами , а зависимые переменные - функциями, откликами, результирующими, объясняемыми.

На практике уравнение регрессии чаще всего подбирается в виде линейной и нелинейной функции (наиболее простые - гипербола, экспонента и парабола) .

Пример 1.3.2. Транспортная задача

Требуется составить план перевозок, при котором все запасы (строительных материалов или конструкций) поставщиков (АБЗ, ЦБЗ, карьеры) будут вывезены, спрос потребителей (объекты дорожных работ, участки) полностью удовлетворен, и при этом суммарные транспортные издержки будут минимальными (стоимость перевозок, сроки, другие ресурсы).

При решении данной задачи составляется система линейных уравнений относительно xij - количества груза (материалов), перевозимого из пункта i в пункт j .

Уравнения в строительной отрасли

Пример 1.4.1. Вычислить стрелу прогиба  (в середине) прямоугольной пластины. Прямоугольная пластина загружена равномерно распределенной нагрузкой интенсивностью q. Пластина защемлена по контуру, края неподвижны .

Стрела прогиба вычисляется как корень нелинейного уравнения на интервале :

Пример 1.4.2. Определить критическую силу для стальной колонны двутаврового сечения, если известны длина колонны L, модуль упругости стали Е, коэффициент жесткости упругой опоры С, момент инерции I.

Критическая сила вычисляется по формуле:

где  - коэффициент приведения длины колонны, который определяется по формуле

Параметр  находится из решения уравнения

на интервале .

ИСПОЛЬЗОВАНИЕ ИНСТРУМЕНТА ПОДБОР ПАРАМЕТРА ПРИ РЕШЕНИИ УРАВНЕНИЙ

При решении производственных задач достаточно часто возникает проблема подбора параметра. Например, в экономических расчётах применяются алгоритмы расчёта стоимости товара, расчёта фонда заработной платы, прибыли от деятельности предприятия, которые, в свою очередь, зависят от множества изменяемых и неизменяемых факторов .

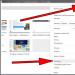
Пример 2.1. Итак, сначала, с целью изучения принципа работы надстройки ПОДБОР ПАРАМЕТРА, рассмотрим решение линейного уравнения вида Ах+В=С с помощью приложения Microsoft Excel.

В ячейку В3 введем любое первоначальное значение переменной x , например, 0, а в ячейку С1 введем левую часть уравнения в виде формулы: =B1*B3+B2. Вызовем диалоговое окно ПОДБОР ПАРАМЕТРА с помощью команд Данные - Анализ «что-если» - Подбор параметра . В этом окне в поле Установить в ячейке введем ссылку на ячейку с формулой, в поле Значение - ожидаемый результат (т.е. 7), в поле Изменяя значение в ячейке - ссылку на ячейку, в которой будет храниться значение подбираемого параметра (содержимое этой ячейки не может быть формулой).

Рисунок 1 - Диалоговое окно ПОДБОР ПАРМЕТРА

После нажатия кнопки ОК , получим результат.

Рисунок 2 - Решение линейного уравнения с помощью диалогового окна ПОДБОР ПАРАМЕТРА

Известно, что инструмент Подбор параметра в основном используется при решении линейного уравнения. Если пытаться, например, решать с помощью Подбора параметра квадратное уравнение (которое имеет два корня), то инструмент найдет решение, но только одно, то, которое ближе к начальному значению.

Пример 2.2. Рассмотрим пример решения квадратного уравнения. Найдем корни квадратного уравнения. Сначала создадим первоначальную таблицу.

Рисунок 3 - Первоначальные данные квадратного уравнения

Зададим любое первоначальное значение х, например, 0. Далее воспользуемся инструментом ПОДБОР ПАРАМЕТРА .

Получили результат: 2.

Второй корень найдем, задав другое начальное значение, например, 5. И проделаем те же действия.

ИСПОЛЬЗОВАНИЕ НАДСТРОЙКИ ПОИСК РЕШЕНИЯ ПРИ РЕШЕНИИ УРАВНЕНИЙ

Пример 3.1. Рассмотрим решение квадратного уравнения (с предыдущей главы) с помощью инструмента ПОИСК РЕШЕНИЯ.

Введем начальные данные

Рисунок 4 - Первоначальные данные квадратного уравнения

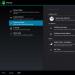
Вызываем инструмент ПОИК РЕШЕНИЯ, выбрав команду ДАННЫЕ.

Рисунок 5 - Надстройка ПОИСК РЕШЕНИЯ при решении квадратного уравнения

В поле «Установить целевую ячейку» выбираем ячейку с формулой квадратного уравнения С1. Далее установим переключатель в положение «Равной значению 0». В поле «Изменяя ячейки» добавим ячейку В4. Нажмем кнопку «Выполнить». Получили решение.

Рисунок 6 - Решение квадратного уравнения, найденного с помощью надстройки ПОИСК РЕШЕНИЯ

При решении данным способом также получили только один корень.

Для нахождения второго корня зададим другое начальное значение переменной х, например, равно 1.

Однако, на любом производстве чаще всего приходится сталкиваться с уравнениями высших степеней .

Пример 3.2. Рассмотрим уравнение пятой степени -3x 5 +x 3 +2x 2 -3x-3=0.

Прежде чем находить корни уравнения (а у этого уравнения должно быть максимум 5 корней), выясним, в каких интервалах содержатся эти корни. Воспользуемся графиком функции, с помощью которого мы наглядно увидим промежутки расположения корней уравнения.

Построим график функции. Для этого в ячейке А1 введем «х», в ячейке В1 введем «у». Значения х внесем в ячейки А2:А22, значения у будем рассчитывать в ячейках В2:В22 соответственно.

Рисунок 7 - Формула уравнения пятой степени

Известно, что корень уравнения (уравнение записано в виде f(x )=0) - это такое значение аргумента, при котором значение функции равно нулю. В графическом представлении - это может быть точка пересечения или касания графика функции с осью абсцисс.

Построим график функции.

Рисунок 8 - График функции на промежутке [-10; 10] с шагом 1

График функции показывает, что уравнение, имеет единственный действительный корень (остальные - комплексные), который находится в промежутке [-1; 0].

Найдем его с помощью инструмента ПОИСК РЕШЕНИЯ. Для этого в таблице выберем точку, близкую к решению уравнения, например, -0,7.

Рисунок 9 - Нахождение корня уравнения с помощью надстройки

ПОИСК РЕШЕНИЯ

Установим с помощью команды «Формат ячеек» относительную погрешность 0,0001.

Итак, решением уравнения является х≈ -0,668.

Таким образом, получили алгоритм решения уравнения высшей степени:

поиск интервалов, в которых содержится только по одному корню;

уточнение корня в выбранном интервале (определением значения корня с заданной точностью).

Тригонометрические уравнения

Особенность тригонометрических уравнений заключается в том, что они имеют бесконечно много решений, и все решения отличаются между собой на определенный период.

Пример решения одного из тригонометрических уравнений подробно рассмотрен в Приложении 1.

В Приложении 2 также рассмотрен пример нахождения решений системы линейных уравнений.

ЗАКЛЮЧЕНИЕ

В результате проведенной исследовательской работы было выявлено, что решение различных уравнений и систем уравнений применяется во многих отраслях экономики и промышленности.

В ходе исследований мы научились находить корни уравнений и систем линейных уравнений с помощью инструментов ПОИСК РЕШЕНИЯ и ПОДБОР ПАРАМЕТРА приложения Microsoft Excel, создали видеокурсы по решению уравнений с помощью приложения Microsoft Excel.

Таким образом, поставленные цель и задачи данного исследования были выполнены.

Кроме того, экспериментальным путём, было выявлено, что использование инструментов ПОИСК РЕШЕНИЯ и ПОДБОР ПАРАМЕТРА приложения Microsoft Excel значительно упрощает процесс нахождения корней уравнений и систем уравнений. Таким образом, поставленная в начале исследования гипотеза подтвердилась.

Результаты выполненной работы позволят использовать возможности изученных инструментов в будущей профессиональной деятельности, особенно если выполнение задания будет содержать сложные расчеты.

Исследование может быть полезно не только учащимся в учебной деятельности, но и специалистам различных отраслей экономики и промышленности, занимающимся проектированием объектов.

Результаты проведенной работы могут быть использованы при изучении других возможностей приложения Microsoft Excel.

На этом исследование не закончено. Мы планируем продолжить рассмотреть способы решения систем нелинейных уравнений с помощью Microsoft Excel.

СПИСОК ИСПОЛЬЗОВАННЫХ ИСТОЧНИКОВ И ЛИТЕРАТУРЫ:

Богомолов, С.В. Экономико-математические методы проектирования транспортных сооружений [Электронный ресурс] : методические указания к практическим занятиям и самостоятельной работе для студентов специальности 270205 «Автомобильные дороги и аэродромы» всех форм обучения / С.В. Богомолов. - Электрон. дан. - Кемерово: КуГТУ, 2013. - 30 с.

Информатика для экономистов. Практикум: учебное пособие для бакалавров / под ред. В.П. Полякова, В.П. Косарева. - М.: Издательство Юрайт, 2013. - 343 с.

Митрофанов, С.В. Использование системы MathCAD при решении задач электротехники и электромеханики: методические указания к выполнению РГЗ по дисциплине «Прикладные задачи программирования» / С.В. Митрофанов, А.С. Падеев. - Оренбург: ГОУ ОГУ, 2005. - 40 с.

Репкин, Д.А. Применение MS EXCEL для решения прикладных задач в экономике: учебное пособие для студентов направления 080100 «Экономика» всех профилей подготовки, всех форм обучения / Д.А. Репкин. - Киров: ПРИП ФГБОУ ВПО «ВятГУ», 2012. [Электронный ресурс]

Федулов, С.В. Использование MS Excel в финансовых вычислениях: учеб.-метод. пособие / С.В. Федулов. - Екатеринбург: Изд-во УрГУПС, 2013. - 94 с.

Численные методы. Часть 1: Методические указания к лабораторным и самостоятельным работам по курсам «Информатика» и «Вычислительная математика» / Сост. Ф.Г. Ахмадиев, Ф.Г. Габбасов, Р.Ф. Гизяятов, И.В. Маланичев. - Казань: Изд-во казан. гос. архитект-строит. ун-та, 2013 - 34 с.

Решение нелинейных уравнений в Excel https://www.altstu.ru/media/f/lr3nelin-uravn.pdf - сайт Алтайского государственного технического университета им. И.И. Ползунова

http://excel2.ru/articles/podbor-parametra-v-ms-excel - сайт Excel2.ru

https://knowledge.allbest.ru/mathematics/3c0b65625b3ad68b4c43a89421306d37_0.html - сайт allbest

Приложение 1

Решение тригонометрического уравнения с помощью инструмента ПОИСК РЕШЕНИЯ

Найдем решения уравнения.

Решать данное уравнение будем аналогично примеру 3.1. То есть:

Протабулируем функцию и построим ее график;

Уточним корни уравнения.

Протабулируем функцию на промежутке [-10; 10]. Сначала в ячейках А2:А22 зададим значения аргумента x и найдем значения функции в данных точках, которые запишем в ячейки В2:В22.

В ячейке В2 укажем формулу: =A2*TAN(A2)-1

Рисунок 1 - Таблица значений аргумента и функции

на отрезке [-10; 10] с шагом 1

Построим график функции на данном отрезке.

Рисунок 2 - График заданной тригонометрической фнкции

Проанализировав график и таблицу значений функции, видим, что корни уравнения расположены в промежутках (-10; -9), (-7; -6); (-4; -3) и т.п., то есть на тех промежутках, где функция меняет знак и пересекает ось Ох.

Уточним первый корень уравнения. Для этого установим курсор в ячейке В2 и вызовем инструмент ПОИСК РЕШЕНИЯ.

Рисунок 3 - Надстройка ПОИСК РЕШЕНИЯ

Итак, первый корень получен.

Рисунок 4 - Решение тригонометрического уравнения

Аналогично, найдем корень уравнения, задав начальное значение х=-7 и х= -4.

Рисунок 5 - Три корня тригонометрического уравнения

Учитывая, что период функции тангенса равен π, найдем разницу между корнями уравнения: получили 3,04 и 3,01. Итак, разность между корнями равна примерно 3. Следовательно, следующие корни уравнения: - 0,4; 2,6; и т.п.

Таким образом, для нахождения корней тригонометрического уравнения, необходимо проделать те же действия, что и при решении уравнений высших степеней.

Приложение 2

Использование инструмента ПОИСК РЕШЕНИЯ при решении систем линейных уравнений

С помощью инструмента ПОИСК РЕШЕНИЯ можно решить и систему линейных уравнений .

Пример 4.1. Решим следующую систему линейных уравнений

Для этого зададим ячейки, где будут записаны решения системы уравнений. Пусть это будут ячейки A2:D2.

Рисунок 1 - Создание таблицы для решения системы линейных уравнений

Введем в ячейки, предназначенные для решения (А2:D2) произвольные величины, лежащие в области определения (начальные значения).

В ячейки (А3:D3) внесем формулы, по которым должны вычисляться правые части уравнений: (=8*A2+4*B2-6*C2; =-2*А2-4*С2-6*D2; =6*А2+4*В2+4*С2+6*D2; = 4*А2+6*В2+8*С2+8*D2)

Рисунок 2 - Первоначальная таблица для решения системы линейных уравнений

Запустим ПОИСК РЕШЕНИЯ из меню ДАННЫЕ. Выберем одну из ячеек, содержащих формулы, в качестве целевой ячейки (например, А3), сделаем её равной -18.

В поле ИЗМЕНЯЯ ЯЧЕЙКИ вставим ячейки А2:D2. Добавим ограничения, нажимая на кнопку ДОБАВИТЬ: В3=-2; С3=-14; D3=-6.

Рисунок 3 - Диалоговое окно надстройки ПОИСК РЕШЕНИЯ

Рисунок 4 - Диалоговое окно ДОБАВЛЕНИЕ ОГРАНИЧЕНИЯ

Нажмем на кнопку ВЫПОЛНИТЬ. Получим решение:

Рисунок 5 - Решение системы линейных уравнений

Таким образом, решение системы линейных уравнений найдено. Если проверить решение (х1=-5, х2=1, х3=-3, х4=4) подстановкой, то получим верные равенства.

Большинство задач, решаемых с помощью электронной таблицы, предполагают нахождение искомого результата по известным исходным данным. Но в Excel есть инструменты, позволяющие решить и обратную задачу: подобрать исходные данные для получения желаемого результата.

Одним из таких инструментов является Поиск решения , который особенно удобен для решения так называемых "задач оптимизации".

Если Вы раньше не использовали Поиск решения , то Вам потребуется установить соответствующую надстройку.

Сделать это можно так:

для версий старше Excel 2007 через команду меню Сервис --> Надстройки;

начиная с Excel 2007 через диалоговое окно Параметры Excel

Начиная с версии Excel 2007 кнопка для запуска Поиска решения появится на вкладке Данные .

В версиях до Excel 2007 аналогичная команда появится в меню Сервис

Разберём порядок работы Поиска решения на простом примере.

Пример 1. Распределение премии

Предположим, что Вы начальник производственного отдела и Вам предстоит по-честному распределить премию в сумме 100 000 руб. между сотрудниками отдела пропорционально их должностным окладам. Другими словами Вам требуется подобрать коэффициент пропорциональности для вычисления размера премии по окладу.

Первым делом создаём таблицу с исходными данными и формулами, с помощью которых должен быть получен результат. В нашем случае результат - это суммарная величина премии. Очень важно, чтобы целевая ячейка (С8) посредством формул была связана с искомой изменяемой ячейкой (Е2). В примере они связаны через промежуточные формулы, вычисляющие размер премии для каждого сотрудника (С2:С7).

Теперь запускаем Поиск решения и в открывшемся диалоговом окне устанавливаем необходимые параметры. Внешний вид диалоговых окон в разных версиях несколько различается:

Начиная с Excel 2010

До Excel 2010

После нажатия кнопки Найти решение (Выполнить) Вы уже можете видеть в таблице полученный результат. При этом на экране появляется диалоговое окно Результаты поиска решения.

Начиная с Excel 2010

До Excel 2010

Если результат, который Вы видите в таблице Вас устраивает, то в диалоговом окне Результаты поиска решения нажимаете ОК и фиксируете результат в таблице. Если же результат Вас не устроил, то нажимаете Отмена и возвращаетесь к предыдущему состоянию таблицы.

Решение данной задачи выглядит так

Важно: при любых изменениях исходных данных для получения нового результата Поиск решения придется запускать снова.

Разберём еще одну задачу оптимизации (получение максимальной прибыли)

Пример 2. Мебельное производство (максимизация прибыли)

Фирма производит две модели А и В сборных книжных полок.

Их производство ограничено наличием сырья (высококачественных досок) и временем машинной обработки.

Для каждого изделия модели А требуется 3 м² досок, а для изделия модели В - 4 м². Фирма может получить от своих поставщиков до 1700 м² досок в неделю.

Для каждого изделия модели А требуется 12 мин машинного времени , а для изделия модели В - 30 мин. в неделю можно использовать 160 ч машинного времени.

Сколько изделий каждой модели следует выпускать фирме в неделю для достижения максимальной прибыли, если каждое изделие модели А приносит 60 руб. прибыли, а каждое изделие модели В - 120 руб. прибыли?

Порядок действий нам уже известен.

Сначала создаем таблицы с исходными данными и формулами. Расположение ячеек на листе может быть абсолютно произвольным, таким как удобно автору. Например, как на рисунке

Запускаем Поиск решения и в диалоговом окне устанавливаем необходимые параметры

1. Целевая ячейка B12 содержит формулу для расчёта прибыли
2. Параметр оптимизации - максимум
3. Изменяемые ячейки B9:C9
4. Ограничения: найденные значения должны быть целыми, неотрицательными; общее количество машинного времени не должно превышать 160 ч (ссылка на ячейку D16); общее количество сырья не должно превышать 1700 м² (ссылка на ячейку D15). Здесь вместо ссылок на ячейки D15 и D16 можно было указать числа, но при использовании ссылок какие-либо изменения ограничений можно производить прямо в таблице
5. Нажимаем кнопку Найти решение (Выполнить) и после подтверждения получаем результат

Но даже если Вы правильно создали формулы и задали ограничения, результат может оказаться неожиданным. Например, при решении данной задачи Вы можете увидеть такой результат:

И это несмотря на то, что было задано ограничение целое . В таких случаях можно попробовать настроить параметры Поиска решения . Для этого в окне Поиск решения нажимаем кнопку Параметры и попадаем в одноимённое диалоговое окно

Первый из выделенных параметров отвечает за точность вычислений. Уменьшая его, можно добиться более точного результата, в нашем случае - целых значений. Второй из выделенных параметров (доступен, начиная с версии Excel 2010) даёт ответ на вопрос: как вообще могли получиться дробные результаты при ограничении целое ? Оказывается Поиск решения это ограничение просто проигнорировал в соответствии с установленным флажком.

Пример 3. Транспортная задача (минимизация затрат)

На заказ строительной компании песок перевозиться от трех поставщиков (карьеров) пяти потребителям (строительным площадкам). Стоимость на доставку включается в себестоимость объекта, поэтому строительная компания заинтересована обеспечить потребности своих стройплощадок в песке самым дешевым способом.

Дано: запасы песка на карьерах; потребности в песке стройплощадок; затраты на транспортировку между каждой парой «поставщик-потребитель».

Нужно найти схему оптимальных перевозок для удовлетворения нужд (откуда и куда), при которой общие затраты на транспортировку были бы минимальными.

Пример расположения ячеек с исходными данными и ограничениями, искомых ячеек и целевой ячейки показан на рисунке

В серых ячейках формулы суммы по строкам и столбцам, а в целевой ячейке формула для подсчёта общих затрат на транспортировку .

Запускаем Поиск решения и устанавливаем необходимые параметры (см. рисунок)

Нажимаем Найти решение (Выполнить) и получаем результат, изображенный ниже

В заключение предлагаю попробовать свои силы в применении Поиска решения и решить с его помощью старинную задачу:

Крестьянин на базаре за 100 рублей купил 100 голов скота. Бык стоит 10 рублей, корова 5 рублей, телёнок 50 копеек. Сколько быков, коров и телят купил крестьянин?

Умение решать системы уравнений часто может принести пользу не только в учебе, но и на практике. В то же время, далеко не каждый пользователь ПК знает, что в Экселе существует собственные варианты решений линейных уравнений. Давайте узнаем, как с применением инструментария этого табличного процессора выполнить данную задачу различными способами.

Способ 1: матричный метод

Самый распространенный способ решения системы линейных уравнений инструментами Excel – это применение матричного метода. Он заключается в построении матрицы из коэффициентов выражений, а затем в создании обратной матрицы. Попробуем использовать данный метод для решения следующей системы уравнений:

14x1 +2x2 +8x4 =218
7x1 -3x2 +5x3 +12x4 =213
5x1 +x2 -2x3 +4x4 =83
6x1 +2x2 +x3 -3x4 =21

1. Заполняем матрицу числами, которые являются коэффициентами уравнения. Данные числа должны располагаться последовательно по порядку с учетом расположения каждого корня, которому они соответствуют. Если в каком-то выражении один из корней отсутствует, то в этом случае коэффициент считается равным нулю. Если коэффициент не обозначен в уравнении, но соответствующий корень имеется, то считается, что коэффициент равен 1 . Обозначаем полученную таблицу, как вектор A .



2. Отдельно записываем значения после знака «равно». Обозначаем их общим наименованием, как вектор B .



3. Теперь для нахождения корней уравнения, прежде всего, нам нужно отыскать матрицу, обратную существующей. К счастью, в Эксель имеется специальный оператор, который предназначен для решения данной задачи. Называется он МОБР . Он имеет довольно простой синтаксис:

   МОБР(массив)

   Аргумент «Массив» — это, собственно, адрес исходной таблицы.

   Итак, выделяем на листе область пустых ячеек, которая по размеру равна диапазону исходной матрицы. Щелкаем по кнопке «Вставить функцию» , расположенную около строки формул.



4. Выполняется запуск Мастера функций . Переходим в категорию «Математические» . В представившемся списке ищем наименование «МОБР» . После того, как оно отыскано, выделяем его и жмем на кнопку «OK» .



5. МОБР . Оно по числу аргументов имеет всего одно поле – «Массив» . Тут нужно указать адрес нашей таблицы. Для этих целей устанавливаем курсор в это поле. Затем зажимаем левую кнопку мыши и выделяем область на листе, в которой находится матрица. Как видим, данные о координатах размещения автоматически заносятся в поле окна. После того, как эта задача выполнена, наиболее очевидным было бы нажать на кнопку «OK» , но не стоит торопиться. Дело в том, что нажатие на эту кнопку является равнозначным применению команды Enter . Но при работе с массивами после завершения ввода формулы следует не кликать по кнопке Enter , а произвести набор сочетания клавиш Ctrl+Shift+Enter . Выполняем эту операцию.



6. Итак, после этого программа производит вычисления и на выходе в предварительно выделенной области мы имеем матрицу, обратную данной.



7. Теперь нам нужно будет умножить обратную матрицу на матрицу B , которая состоит из одного столбца значений, расположенных после знака «равно» в выражениях. Для умножения таблиц в Экселе также имеется отдельная функция, которая называется МУМНОЖ . Данный оператор имеет следующий синтаксис:

   МУМНОЖ(Массив1;Массив2)

   Выделяем диапазон, в нашем случае состоящий из четырех ячеек. Далее опять запускаем Мастер функций , нажав значок «Вставить функцию» .



8. В категории «Математические» , запустившегося Мастера функций , выделяем наименование «МУМНОЖ» и жмем на кнопку «OK» .



9. Активируется окно аргументов функции МУМНОЖ . В поле «Массив1» заносим координаты нашей обратной матрицы. Для этого, как и в прошлый раз, устанавливаем курсор в поле и с зажатой левой кнопкой мыши выделяем курсором соответствующую таблицу. Аналогичное действие проводим для внесения координат в поле «Массив2» , только на этот раз выделяем значения колонки B . После того, как вышеуказанные действия проведены, опять не спешим жать на кнопку «OK» или клавишу Enter , а набираем комбинацию клавиш Ctrl+Shift+Enter .



10. После данного действия в предварительно выделенной ячейке отобразятся корни уравнения: X1 , X2 , X3 и X4 . Они будут расположены последовательно. Таким образом, можно сказать, что мы решили данную систему. Для того, чтобы проверить правильность решения достаточно подставить в исходную систему выражений данные ответы вместо соответствующих корней. Если равенство будет соблюдено, то это означает, что представленная система уравнений решена верно.



Способ 2: подбор параметров

Второй известный способ решения системы уравнений в Экселе – это применение метода подбора параметров. Суть данного метода заключается в поиске от обратного. То есть, основываясь на известном результате, мы производим поиск неизвестного аргумента. Давайте для примера используем квадратное уравнение






Этот результат также можно проверить, подставив данное значение в решаемое выражение вместо значения x .

Способ 3: метод Крамера

Теперь попробуем решить систему уравнений методом Крамера. Для примера возьмем все ту же систему, которую использовали в Способе 1 :

14x1 +2x2 +8x4 =218
7x1 -3x2 +5x3 +12x4 =213
5x1 +x2 -2x3 +4x4 =83
6x1 +2x2 +x3 -3x4 =21


1. Как и в первом способе, составляем матрицу A из коэффициентов уравнений и таблицу B из значений, которые стоят после знака «равно» .



2. Далее делаем ещё четыре таблицы. Каждая из них является копией матрицы A , только у этих копий поочередно один столбец заменен на таблицу B . У первой таблицы – это первый столбец, у второй таблицы – второй и т.д.



3. Теперь нам нужно высчитать определители для всех этих таблиц. Система уравнений будет иметь решения только в том случае, если все определители будут иметь значение, отличное от нуля. Для расчета этого значения в Экселе опять имеется отдельная функция – МОПРЕД . Синтаксис данного оператора следующий:

   МОПРЕД(массив)

   Таким образом, как и у функции МОБР , единственным аргументом выступает ссылка на обрабатываемую таблицу.

   Итак, выделяем ячейку, в которой будет выводиться определитель первой матрицы. Затем жмем на знакомую по предыдущим способам кнопку «Вставить функцию» .



4. Активируется окно Мастера функций . Переходим в категорию «Математические» и среди списка операторов выделяем там наименование «МОПРЕД» . После этого жмем на кнопку «OK» .



5. Запускается окно аргументов функции МОПРЕД . Как видим, оно имеет только одно поле – «Массив» . В это поле вписываем адрес первой преобразованной матрицы. Для этого устанавливаем курсор в поле, а затем выделяем матричный диапазон. После этого жмем на кнопку «OK» . Данная функция выводит результат в одну ячейку, а не массивом, поэтому для получения расчета не нужно прибегать к нажатию комбинации клавиш Ctrl+Shift+Enter .



6. Функция производит подсчет результата и выводит его в заранее выделенную ячейку. Как видим, в нашем случае определитель равен -740 , то есть, не является равным нулю, что нам подходит.



7. Аналогичным образом производим подсчет определителей для остальных трех таблиц.



8. На завершающем этапе производим подсчет определителя первичной матрицы. Процедура происходит все по тому же алгоритму. Как видим, определитель первичной таблицы тоже отличный от нуля, а значит, матрица считается невырожденной, то есть, система уравнений имеет решения.



9. Теперь пора найти корни уравнения. Корень уравнения будет равен отношению определителя соответствующей преобразованной матрицы на определитель первичной таблицы. Таким образом, разделив поочередно все четыре определителя преобразованных матриц на число -148 , которое является определителем первоначальной таблицы, мы получим четыре корня. Как видим, они равны значениям 5 , 14 , 8 и 15 . Таким образом, они в точности совпадают с корнями, которые мы нашли, используя обратную матрицу в способе 1 , что подтверждает правильность решения системы уравнений.



Способ 4: метод Гаусса

Решить систему уравнений можно также, применив метод Гаусса. Для примера возьмем более простую систему уравнений из трех неизвестных:

14x1 +2x2 +8x3 =110
7x1 -3x2 +5x3 =32
5x1 +x2 -2x3 =17


1. Опять последовательно записываем коэффициенты в таблицу A , а свободные члены, расположенные после знака «равно» — в таблицу B . Но на этот раз сблизим обе таблицы, так как это понадобится нам для работы в дальнейшем. Важным условием является то, чтобы в первой ячейке матрицы A значение было отличным от нуля. В обратном случае следует переставить строки местами.



2. Копируем первую строку двух соединенных матриц в строчку ниже (для наглядности можно пропустить одну строку). В первую ячейку, которая расположена в строке ещё ниже предыдущей, вводим следующую формулу:

   B8:E8-$B$7:$E$7*(B8/$B$7)

   Если вы расположили матрицы по-другому, то и адреса ячеек формулы у вас будут иметь другое значение, но вы сможете высчитать их, сопоставив с теми формулами и изображениями, которые приводятся здесь.

   После того, как формула введена, выделите весь ряд ячеек и нажмите комбинацию клавиш Ctrl+Shift+Enter . К ряду будет применена формула массива и он будет заполнен значениями. Таким образом мы произвели вычитание из второй строки первой, умноженной на отношение первых коэффициентов двух первых выражений системы.



3. После этого копируем полученную строку и вставляем её в строчку ниже.



4. Выделяем две первые строки после пропущенной строчки. Жмем на кнопку «Копировать» , которая расположена на ленте во вкладке «Главная» .



5. Пропускаем строку после последней записи на листе. Выделяем первую ячейку в следующей строке. Кликаем правой кнопкой мыши. В открывшемся контекстном меню наводим курсор на пункт «Специальная вставка» . В запустившемся дополнительном списке выбираем позицию «Значения» .



6. В следующую строку вводим формулу массива. В ней производится вычитание из третьей строки предыдущей группы данных второй строки, умноженной на отношение второго коэффициента третьей и второй строки. В нашем случае формула будет иметь следующий вид:

   B13:E13-$B$12:$E$12*(C13/$C$12)

   После ввода формулы выделяем весь ряд и применяем сочетание клавиш Ctrl+Shift+Enter .



7. Теперь следует выполнить обратную прогонку по методу Гаусса. Пропускаем три строки от последней записи. В четвертой строке вводим формулу массива:

   Таким образом, мы делим последнюю рассчитанную нами строку на её же третий коэффициент. После того, как набрали формулу, выделяем всю строчку и жмем сочетание клавиш Ctrl+Shift+Enter .



8. Поднимаемся на строку вверх и вводим в неё следующую формулу массива:

   =(B16:E16-B21:E21*D16)/C16

   Жмем привычное уже нам сочетание клавиш для применения формулы массива.



9. Поднимаемся ещё на одну строку выше. В неё вводим формулу массива следующего вида:

   =(B15:E15-B20:E20*C15-B21:E21*D15)/B15

   Опять выделяем всю строку и применяем сочетание клавиш Ctrl+Shift+Enter .



10. Теперь смотрим на числа, которые получились в последнем столбце последнего блока строк, рассчитанного нами ранее. Именно эти числа (4 , 7 и 5 ) будут являться корнями данной системы уравнений. Проверить это можно, подставив их вместо значений X1 , X2 и X3 в выражения.



Как видим, в Экселе систему уравнений можно решить целым рядом способов, каждый из которых имеет собственные преимущества и недостатки. Но все эти методы можно условно разделить на две большие группы: матричные и с применением инструмента подбора параметров. В некоторых случаях не всегда матричные методы подходят для решения задачи. В частности тогда, когда определитель матрицы равен нулю. В остальных же случаях пользователь сам волен решать, какой вариант он считает более удобным для себя.

Пользователи Excel давно и успешно применяют программу для решения различных типов задач в разных областях.

Excel – это самая популярная программа в каждом офисе во всем мире. Ее возможности позволяют быстро находить эффективные решения в самых разных сферах деятельности. Программа способна решать различного рода задачи: финансовые, экономические, математические, логические, оптимизационные и многие другие. Для наглядности мы каждое из выше описанных решение задач в Excel и примеры его выполнения.

Решение задач оптимизации в Excel

Оптимизационные модели применяются в экономической и технической сфере. Их цель – подобрать сбалансированное решение, оптимальное в конкретных условиях (количество продаж для получения определенной выручки, лучшее меню, число рейсов и т.п.).

В Excel для решения задач оптимизации используются следующие команды:

Для решения простейших задач применяется команда «Подбор параметра». Самых сложных – «Диспетчер сценариев». Рассмотрим пример решения оптимизационной задачи с помощью надстройки «Поиск решения».

Условие. Фирма производит несколько сортов йогурта. Условно – «1», «2» и «3». Реализовав 100 баночек йогурта «1», предприятие получает 200 рублей. «2» - 250 рублей. «3» - 300 рублей. Сбыт, налажен, но количество имеющегося сырья ограничено. Нужно найти, какой йогурт и в каком объеме необходимо делать, чтобы получить максимальный доход от продаж.

Известные данные (в т.ч. нормы расхода сырья) занесем в таблицу:

На основании этих данных составим рабочую таблицу:

1. Количество изделий нам пока неизвестно. Это переменные.
2. В столбец «Прибыль» внесены формулы: =200*B11, =250*В12, =300*В13.
3. Расход сырья ограничен (это ограничения). В ячейки внесены формулы: =16*B11+13*B12+10*B13 («молоко»); =3*B11+3*B12+3*B13 («закваска»); =0*B11+5*B12+3*B13 («амортизатор») и =0*B11+8*B12+6*B13 («сахар»). То есть мы норму расхода умножили на количество.
4. Цель – найти максимально возможную прибыль. Это ячейка С14.

Активизируем команду «Поиск решения» и вносим параметры.

После нажатия кнопки «Выполнить» программа выдает свое решение.

Оптимальный вариант – сконцентрироваться на выпуске йогурта «3» и «1». Йогурт «2» производить не стоит.



Решение финансовых задач в Excel

Чаще всего для этой цели применяются финансовые функции. Рассмотрим пример.

Оформим исходные данные в виде таблицы:

Так как процентная ставка не меняется в течение всего периода, используем функцию ПС (СТАВКА, КПЕР, ПЛТ, БС, ТИП).

Заполнение аргументов:

1. Ставка – 20%/4, т.к. проценты начисляются ежеквартально.
2. Кпер – 4*4 (общий срок вклада * число периодов начисления в год).
3. Плт – 0. Ничего не пишем, т.к. депозит пополняться не будет.
4. Тип – 0.
5. БС – сумма, которую мы хотим получить в конце срока вклада.

Вкладчику необходимо вложить эти деньги, поэтому результат отрицательный.

Для проверки правильности решения воспользуемся формулой: ПС = БС / (1 + ставка) кпер. Подставим значения: ПС = 400 000 / (1 + 0,05) 16 = 183245.

Решение эконометрики в Excel

Для установления количественных и качественных взаимосвязей применяются математические и статистические методы и модели.

Дано 2 диапазона значений:

Значения Х будут играть роль факторного признака, Y – результативного. Задача – найти коэффициент корреляции.

Для решения этой задачи предусмотрена функция КОРРЕЛ (массив 1; массив 2).

Решение логических задач в Excel

В табличном процессоре есть встроенные логические функции. Любая из них должна содержать хотя бы один оператор сравнения, который определит отношение между элементами (=, >, =,

Ученики сдавали зачет. Каждый из них получил отметку. Если больше 4 баллов – зачет сдан. Менее – не сдан.

1. Ставим курсор в ячейку С1. Нажимаем значок функций. Выбираем «ЕСЛИ».
2. Заполняем аргументы. Логическое выражение – B1>=4. Это условие, при котором логическое значение – ИСТИНА.
3. Если ИСТИНА – «Зачет сдал». ЛОЖЬ – «Зачет не сдал».

Решение математических задач в Excel

Средствами программы можно решать как простейшие математические задачки, так и более сложные (операции с функциями, матрицами, линейными уравнениями и т.п.).

Условие учебной задачи. Найти обратную матрицу В для матрицы А.

1. Делаем таблицу со значениями матрицы А.
2. Выделяем на этом же листе область для обратной матрицы.
3. Нажимаем кнопку «Вставить функцию». Категория – «Математические». Тип – «МОБР».
4. В поле аргумента «Массив» вписываем диапазон матрицы А.
5. Нажимаем одновременно Shift+Ctrl+Enter - это обязательное условие для ввода массивов.

Возможности Excel не безграничны. Но множество задач программе «под силу». Тем более здесь не описаны возможности которые можно расширить с помощью макросов и пользовательских настроек.

В этой статье вы узнаете как решить квадратное уравнение в Excel на конкретном примере. Подробно разберем решение несложно задачи с картинками.

Ход решения

Запустим программу Microsoft Office Excel. Я пользуюсь 2007 версией. Для начала объединим ячейки A1:A5 и запишем в них формулу квадратного уравнения в виде ax2+bx+c=0.Далее нам нужно возвести x в квадрат, для этого нужно сделать цифру 2 надстрочным интервалом. Выделим двойку и нажмем правой кнопкой мыши.

Получим формулу вида ax 2 +bx+c=0

В ячейке A2 введем текстовое значение a= , в ячейке A3 b= и в ячейке A4 с= соответственно. Эти значения будут вводиться с клавиатуры в следующих ячейках (B2,B3,B4).

Введем текст для значений, которые будут считаться. В ячейке C2 d=, C3 x 1 = C4 x 2 =. Подстрочный интервал для xсделаем аналогично надстрочному интервалу в x 2

Перейдем к вводу формул для решения

Дискриминант квадратного трехчлена равен b 2 -4ac

В ячейку D2 введем соответствующую формулу для возведения числа во вторую степень:

Квадратное уравнение имеет два корня, в случае если дискриминант больше нуля. В ячейку C3 введем формулу для x 1

ЕСЛИ(D2>0;(-B3+КОРЕНЬ(D2))/(2*B2);»Корней нет»)

Для расчета x2 введем похожую формулу, но со знаком плюс

ЕСЛИ(D2>0;(-B3-КОРЕНЬ(D2))/(2*B2);»Корней нет»)

Соответственно при введенных значениях a,b,c сначала считается дискриминант, если его значения меньше нуля выводится сообщение «Корней нет», иначе получаем значения x 1 и x 2 .

Защита листа в Excel

Нам нужно защитить лист, на котором мы производили расчеты. Без защиты нужно оставить ячейки, в которые можно вводить значения a,b,c, то есть ячейки B2 B3 B4. Для этого выделим данный диапазон и зайдем в формат ячеек, перейдем во вкладку Рецензирования, Защитить лист и уберем флажок с позиции Защищаемая ячейка. Нажмем кнопку OK, подтвердив внесенные изменения.

Этот диапазон ячеек будет не защищен при защите листа. Выполним защиту листа, для этого перейдем на вкладку Рецензирование пункт Защита листа. Пароль наберем 1234. Нажмем OK.

Теперь мы сможем изменять значения ячеек B2,B3,B4. При попытке изменения других ячеек мы получим сообщение следующего содержания: «Ячейка или диаграмма защищена от изменений. А так же совет по снятию защиты.

Так же вас может заинтересовать материал как закрепить .